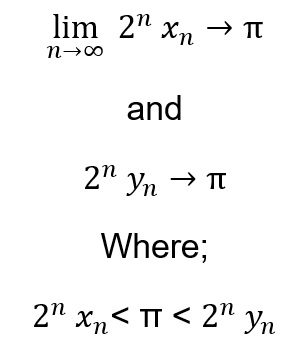The following formulas have been derived using Archimedes method for calculating Pi;
(Lower bound)
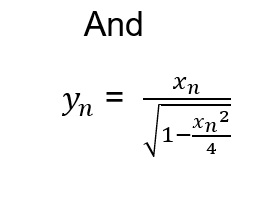
(Upper bound)
Derivations and calculations can be obtained by clicking the formulas or this line.
I have derived the following iteration formulas by adapting Archimedes’ method for calculating Pi (π). I have begun with a square inside a circle for the lower bound and a square outside the circle for the upper bound, then continued doubling the number of sides. By the end of my work I was calculating pi to a specified accuracy by using the difference between my lower bound value and upper bound value. My method assumes no prior knowledge of pi. I believe this work follows on from the author of; https://www.craig-wood.com/nick/articles/pi-archimedes/, who has only derived the lower bound.
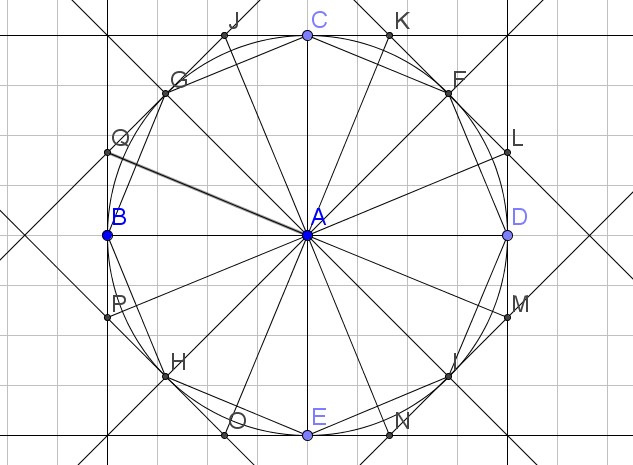
The following diagram shows the geometry used to derive the formulas;
Below are the codes used to check the formulas.
The author’s final Code;
import math
import time
import decimal
from decimal import Decimal, getcontext
print("Calculating a value for pi by considering polygons with increasing numbers of sides")
print("Polygons have been given a fixed diagonal of 2" )
print("___")
n=1
siDe_sQuared=decimal.Decimal(2)
decimalPLaces=100
getcontext().prec=(decimalPLaces*4)
print("The number of sides of this polygon is", 2**(n+1))
pil=decimal.Decimal(siDe_sQuared.sqrt()*(2**(n)))
piu=decimal.Decimal((siDe_sQuared/(1-(siDe_sQuared/4))).sqrt()*(2**n))
error=decimal.Decimal(piu-pil)
print("We have a lower bound value of pi equal to", pil)
print("We have an upper bound value of pi equal to", piu)
print("The error when our upper and lower bounds are subtracted", error)
print("___")
siDe_sQuared=decimal.Decimal(2-2*((1-((siDe_sQuared)/4)).sqrt()))
n=n+1
while piu - pil >= decimal.Decimal(10**-(decimalPLaces+3)):
print("The number of sides of this polygon is", 2**(n+1))
pil=decimal.Decimal(siDe_sQuared.sqrt()*(2**(n)))
piu=decimal.Decimal((siDe_sQuared/(1-(siDe_sQuared/4))).sqrt()*(2**n))
error=decimal.Decimal(piu-pil)
print("We have a lower bound value of pi equal to", pil)
print("We have an upper bound value of pi equal to", piu)
print("The error when our upper and lower bounds are subtracted", error)
print("___")
siDe_sQuared=decimal.Decimal(2-2*((1-((siDe_sQuared)/4)).sqrt()))
n=n+1
else:
print("We are all done we have both values of pi which round correctly to at least ", decimalPLaces , "decimal places. ")
print("Our value of pi rounded to ", decimalPLaces , "decimal places is ", round(pil,decimalPLaces))
time.sleep(2000)
The below code can be found in the article at https://www.craig-wood.com/nick/articles/pi-archimedes/ and uses just the lower bound formula.
import math
import time
import decimal
from decimal import Decimal, getcontext
def pi_archimedes(n):
"""
Calculate n iterations of Archimedes PI recurrence relation
"""
polygon_edge_length_squared = Decimal(2)
polygon_sides = 2
for i in range(n):
polygon_edge_length_squared = 2 - 2 * (1 - polygon_edge_length_squared / 4).sqrt()
polygon_sides *= 2
return polygon_sides * polygon_edge_length_squared.sqrt()
def main():
"""
Try the series
"""
places = 100
old_result = None
for n in range(10*places):
# Do calculations with double precision
getcontext().prec = 2*places
result = pi_archimedes(n)
# Print the result with single precision
getcontext().prec = places
result = +result # do the rounding on result
print("%3d: %s" % (n, result))
if result == old_result:
break
old_result = result
if __name__ == "__main__":
main()